berjilbablah

Attention Please

hari ini , tepatnya setelah sholat dhuhur . Saya di datangi muslimin dari Afganistan , namanya ahmad . Dia berujar pada saya , request my friend to use long skirt ( Menyuruh pakai rok panjang ) . Itu terjadi setelah kami magang 3 hari di AIT. So aku terkejut , tapi tak ada salah jika kita sesama muslim brother , saling menghormati / respect dengan yg lain.
Dengan wajah berewoknya khas orang arab dan bahasa inggris yang lancar . Dia menghimbau agar teman saya berpakaian yg cocok di Masjid , karena itu rumah Allah. So "Iam Understand , I Try say to my Friend to use long skirt" Ring Said . Untung Tak terjadi apa apa. Terima Kasih Saudara , telah remember us.

oke , ne firman Allah tentang Jilbab . Cos saya pun mencari Calon bini , syarat pertama harus beriman dan berjilbab.

Firman Alloh ta’ala dalam surat Al Ahzab ayat 59:

“Wahai Nabi, katakanlah kepada isteri-isterimu dan istri orang-orang beriman, hendaklah mereka mengulurkan jilbabnya ke seluruh tubuh mereka. Yang demikian itu agar mereka lebih mudah untuk dikenal dan tidak diganggu orang. Alloh Maha Pengampun lagi Maha Penyayang.”

Definisi Jilbab

Secara bahasa, dalam kamus al Mu’jam al Wasith 1/128, disebutkan bahwa jilbab memiliki beberapa makna, yaitu:

Qomish (sejenis jubah).
Kain yang menutupi seluruh badan.

Khimar (kerudung).
Pakaian atasan seperti milhafah (selimut).



Semisal selimut (baca: kerudung) yang dipakai seorang wanita untuk menutupi tubuhnya.


Ya , oke karena hidup itu pilihan . Maka berjilbab juga pilihan , dan tetapkan pilihan terbaik yang harus anda jalani . Jangan sampai menyesal karena tak ada flash back life di dunia ini.

Sampai ketemu Lagi .5555
Wassalamualaikum Wr Wb

Read More

Museum Rangsit Science Center Thailand

Halo , ktemu lagi di Thailand Trip dengan Saya . Mr.Ring ( nama pendek saya ) , soalnya orang Thai sulit mengucapkan nama ringga. Mereka biasa memanggil saya ringke , aduh beda banget . Ya uda , jadi ku putuskan memendekkan nama menjadi " Cincin " . Oke hari ini saya akan share mengenai perjalanan di museum. Bila kamu Pelajar , tiket cuma 30 Bath , today 1 bath setara dengan 300 rupiah . Up to you , 30 bath , untuk melihat satu show , kayak bioskop gitu . Tersedia 5 show , kamu bisa pilih apapun , jadi bila kamu mau liat semua show datang lebih pagi sekitar jam 9 . Lokasi tidak jauh dari kampus saya , RMUTT.

Kamu bisa menikmati museum ini . Oke ini isi Museum nya .

lagi Galau.com

Sama Si Botak ( semua pelajar d bawah mahasiswa harus potong kayak tentara , hehehe )

Di Ketawain Kebo Tuh Kamu

Malaikat Penjaga Gerbang

 
View Chatuchak Weekend Market in a larger map

Sorry Sobat , Agak narsis dikit.hehehe . See you , ketemu lagi nanti dengan saya , Mr.Ring . Di Thailand Trip . Ok

Read More

Cronbach's Alpha (α) using SPSS

Introduction

Cronbach's alpha is the most common measure of internal consistency ("reliability"). It is most commonly used when you have multiple Likert questions in a survey/questionnaire that form a scale and you wish to determine if the scale is reliable.

Example

A researcher has devised a nine-question questionnaire with which they hope to measure how safe people feel at work at an industrial complex. Each question was a 5-point Likert item from "strongly disagree" to "strongly agree". In order to understand whether the questions in this questionnaire all reliably measure the same latent variable (feeling of safety) (so a Likert scale could be constructed), a Cronbach's alpha was run on a sample size of 15 workers.

Setup in SPSS

The nine questions have been labelled "Qu1" through to "Qu9". To know how to correctly enter your data into SPSS in order to run a Cronbach's alpha test please read our Entering Data into SPSS tutorial.

Test Procedure in SPSS

1. Click Analyze > Scale > Reliability Analysis... on the top menu as shown below:
   

   Published with written permission from SPSS Inc, an IBM Company.

2. You will be presented with the Reliability Analysis dialogue box:
   

   Published with written permission from SPSS Inc, an IBM Company.

3. Transfer the variables "Qu1" to "Qu9" into the "Items:" box. You can do this by drag-and-dropping the variables into their respective boxes or by using the button. You will be presented with the following screen:
   

   Published with written permission from SPSS Inc, an IBM Company.

4. Leave the "Model:" set as "Alpha", which represents Cronbach's alpha in SPSS. If you want to provide a name for the scale enter it in the "Scale label:" box. Since this only prints the name you enter at the top of the SPSS output, it is certainly not essential that you do; and in this case we will leave it blank.
5. Click on the button, which will present the Reliability Analysis: Statistics dialogue box, as shown below:
   

   Published with written permission from SPSS Inc, an IBM Company.

6. Select the "Item", "Scale" and "Scale if item deleted" in the "Descriptives for" box and "Correlations" in the "Inter-Item" box, as shown below:
   

   Published with written permission from SPSS Inc, an IBM Company.

7. Click the button. This will return you to the Reliability Analysis dialogue box.
8. Click the button to generate the output.

SPSS Output for Cronbach's Alpha

SPSS produces many different tables. The first important table is the Reliability Statistics table that provides the actual value for Cronbach's alpha, as shown below:

Published with written permission from SPSS Inc, an IBM Company.

We can see that in our example, Cronbach's alpha is 0.805, which indicates a high level of internal consistency for our scale with this specific sample.

Item-Total Statistics

The Item-Total Statistics table presents the Cronbach's Alpha if Item Deleted in the final column , as shown below:

Published with written permission from SPSS Inc, an IBM Company.

This column presents the value that Cronbach's alpha would be if that particular item was deleted from the scale. We can see that removal of any question except question 8, would result in a lower Cronbach's alpha. Therefore, we would not want to remove these questions. Removal of question 8 would lead to a small improvement in Cronbach's alpha and we can also see that the Corrected Item-Total Correlation value was low (0.128) for this item. This might lead us to consider whether we should remove this item.

Cronbach's alpha simply provides you with an overall reliability coefficient for a set of variables, e.g. questions. If your questions reflect different underlying personal qualities (or other dimensions), for example, employee motivation and employee commitment, then Cronbach's alpha will not be able to distinguish between these. In order to do this and then check their reliability (using Cronbach's alpha), you will first need to run a test such as a principal components analysis (PCA). If this sounds like something you would want to do, check out the features of our Premium PCA guide, here.

Read More

Cara Menghitung Korelasi dan Menafsirkannya Menggunakan SPSS

Menghitung Korelasi dan menafsirkan menggunakan software SPSS dapat dilakukan dengan cepat dan mudah. Pada artikel kali ini tidak akan dibahas lagi bagaimana rumus korelasi namun lebih kepada langkah praktis bagaimana cara perhitungan dan cara membaca hasilnya dengan program SPSS.

Korelasi merupakan teknik analisis statistik yang sering digunakan oleh peneliti untuk beragam keperluan seperti tugas akhir, skripsi, thesis, disertasi, ataupun penelitian ilmiah lainnya dan termasuk dalam salah satu teknik pengukuran asosiasi atau hubungan (measures of association). Analisis korelasi sering pula dihubungkan dan berkaitan regresi.

Pengukuran asosiasi merupakan istilah umum yang sering digunakan dalam teknik statistik bivariat untuk mengukur kekuatan hubungan antara dua variabel. Diantara beberapa teknik-teknik pengukuran asosiasi, ada dua teknik korelasi yang sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman. Selain kedua teknik tersebut, terdapat pula teknik-teknik korelasi lain, seperti Kendal, Chi-Square, Phi Coefficient, Goodman-Kruskal, Somer, dan Wilson.

Korelasi bermanfaat untuk mengukur kekuatan hubungan antara dua variabel (kadang lebih dari dua variabel) yang terbagi dengan skala-skala tertentu menurut jenis data. Sebagai contoh; Korelasi Pearson menggunakan data berskala interval atau rasio; Spearman dan Kendal menggunakan skala ordinal; Chi Square menggunakan data nominal.

Hasil perhitungan korelasi mempunyai kemungkinan penafsiran terhadap pengujian hipotesis dua arah (two tailed). Korelasi searah jika nilai koefesien korelasi diketemukan positif; sebaliknya jika nilai koefesien korelasi negatif, korelasi disebut tidak searah.

Berikut ini contoh menghitung korelasi dan cara menafsirkannya dengan bantuan software SPSS versi 19.

Misalkan kita memiliki 4 variabel penelitian X1,X2,X3, dan Y. Cara melakukan perhitungan korelasi pearson dengan SPSS 19 adalah sebagai berikut :

• Masukkan data penelitian pada menu SPSS Data editor
  
• Pilih menu Analyze, lalu Correlate, kemudian Bivariate
  
• Pada kotak dialog yang muncul, pilih variabel yang akan diproses dengan meng-klik variabel X1,X2,X3, dan Y dan meng-klik tombol panah (1) yang ada di tengah kotak kiri dan kanan. Nomor (2) dan (3) dipilih berdasarkan perhitungan korelasi yang akan digunakan dan jenis tes signifikansi.
  
• Lihat hasil output di jendela SPSS Output Viewer dan berikan penafsiran atas hasil perhitungan yang muncul.
  

• Penafsiran Hasil Korelasi:
  • Arti Angka Korelasi
    Ada dua tanda dalam penafsiran korelasi melalui nilai koefisien, yaitu tanda (+) dan (-) yang berhubungan dengan arah korelasi, serta menyatakan kuat tidaknya korelasi.
  • Signifikansi Hasil Korelasi
    Berdasarkan nilai Signifikansi, kita bisa mengambil simpulan atas hipotesis :
    H0 = Tidak ada hubungan (korelasi) antara dua variabel.
    H1 = Ada hubungan (korelasi) antara dua variabel.
    Uji dilakukan dua sisi / arah / tailed (ekor).
    Dasar pengambilan keputusan berdasarkan probabilitas menggunakan kriteria :
    - Jika probabilitas > 0,05 (atau 0,01), maka H0 diterima.
    - Jika probabilitas < 0,05 (atau 0,01), maka H0 ditolak.
  Berdasarkan acuan penafsiran diatas, contoh perhitungan korelasi pearson menggunakan data X1,X2, X3, dan Y maka salah satu tafsiran yang dapat kita berikan adalah ;
• Korelasi X1 dan Y memiliki nilai 0,342 yang dapat dikategorikan memiliki hubungan yang lemah dan berdasarkan uji signifikasi hasilnya menunjukkan nilai 0,140 yang berarti asosiasi kedua variabel adalah tidak signifikan

Demikian cara menghitung korelasi pearson dengan SPSS 19 dengan contoh korelasi X1-Y. Perhitungan korelasi lainnya seperti korelasi Kendall’s tau-b ataupun korelasi Rank Spearman dapat dilakukan dengan cara yang hampir sama dengan perhitungan korelasi pearson. Tinggal sesuaikan saja jenis data yang dimiliki dengan metoda perhitungan yang tepat.

Artikel lainnya mengenai penjelasan seputar; uji korelasi, regresi dan korelasi, rumus korelasi, korelasi spearman, korelasi spss, statistik korelasi,definisi korelasi, data korelasi, arti korelasi, koefisien korelasi, hubungan korelasi, korelasi penelitian, korelasi statistik, korelasi kanonik, rumus product moment pearson, rumus korelasi pearson, analisis korelasi sederhana, rumus statistik korelasi, analisis korelasi pearson dapat juga dibaca pada referensi berikut :

Buku Latihan SPSS Statistik Parametrik, Singgih Santoso, Elexmedia
http://id.wikipedia.org/wiki/Korelasi
http://www.jonathansarwono.info/korelasi/korelasi.htm

Read More

Contoh Regresi Linier Sederhana dengan SPSS

Artikel ini akan mengupas contoh regresi linier sederhana dengan SPSS menggunakan data regresi menggunakan data yang dipakai seperti pada perhitungan korelasi. Analisis regresi sederhana merupakan salah satu metodi uji regresi yang dapat dipakai sebagai alat inferensi statistik untuk menentukan pengaruh sebuahvariabel bebas (independen) terhadap variabel terikat (dependen).

Regresi linear sederhana ataupun regresi linier berganda pada intinya memiliki beberapa tujuan, yaitu :

• Menghitung nilai estimasi rata-rata dan nilai variabel terikat berdasarkan pada nilai variabel bebas.
• Menguji hipotesis karakteristik dependensi
• Meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas diluar jangkaun sample.

Pada analisis regresi sederhana dengan menggunakan SPSS ada beberapa asumsi dan persyaratan yang perlu diperiksa dan diuji, beberapa diantaranya adalah :

• Variabel bebas tidak berkorelasi dengan disturbance term (Error). Nilai disturbance term sebesar 0 atau dengan simbol sebagai berikut: (E (U / X) = 0,
• Jika variabel bebas lebih dari satu, maka antara variabel bebas (explanatory) tidak ada hubungan linier yang nyata,
• Model regresi dikatakan layak jika angka signifikansi pada ANOVA sebesar < 0.05,
• Predictor yang digunakan sebagai variabel bebas harus layak. Kelayakan ini diketahui jika angka Standard Error of Estimate < Standard Deviation,
• Koefisien regresi harus signifikan. Pengujian dilakukan dengan Uji T. Koefesien regresi signifikan jika T hitung > T table (nilai kritis),
• Model regresi dapat diterangkan dengan menggunakan nilai koefisiena determinasi (KD = r² x 100%) semakin besar nilai tersebut maka model semakin baik. Jika nilai mendekati 1 maka model regresi semakin baik,
• Data harus berdistribusi normal,
• Data berskala interval atau rasio,
• Kedua variabel bersifat dependen, artinya satu variabel merupakan variabel bebas (variabel predictor) sedang variabel lainnya variabel terikat (variabel response)

Berikut ini contoh perhitungan regresi linier sederhana menggunakan software SPSS 19.

• Dengan menggunakan data yang sama seperti pada artikel perhitungan korelasi, proses mulai dengan memilih menu Analyze, kemudian pilih Linear,
  
• Pilih variabel Y sebagai variabel dependen (terikat) dan X1 sebagai variabel independen (bebas) lalu klik tombol OK,
  
• Output SPSS akan menampilkan hasil berupa 4 buah tabel yaitu; 1.) tabel variabel penelitian, 2.) ringkasan model (model summary), 3.) Tabel Anova, dan 4.) Tabel Koefisien.
  
• Cara membaca output spss hasil uji regresi linier tersebut adalah :
  • Tabel pertama menunjukkan variabel apa saja yang diproses, mana yang menjadi variabel bebas dan variabel terikat.
  • Tabel kedua menampilkan nilai R yang merupakan simbol dari nilai koefisien korelasi. Pada contoh diatas nilai korelasi adalah 0,342. Nilai ini dapat diinterpretasikan bahwa hubungan kedua variabel penelitian ada di kategori lemah.
    Melalui tabel ini juga diperoleh nilai R Square atau koefisien determinasi (KD) yang menunjukkan seberapa bagus model regresi yang dibentuk oleh interaksi variabel bebas dan variabel terikat. Nilai KD yang diperoleh adalah 11,7% yang dapat ditafsirkan bahwa variabel bebas X1 memiliki pengaruh kontribusi sebesar 11,7% terhadap variabel Y dan 88,3% lainnya dipengaruhi oleh faktor-faktor lain diluar variabel X1.
  • Tabel ketiga digunakan untuk menentukan taraf signifikansi atau linieritas dari regresi. Kriterianya dapat ditentukan berdasarkan uji F atau uji nilai Signifikansi (Sig.). Cara yang paling mudah dengan uji Sig., dengan ketentuan, jika Nilai Sig. < 0,05, maka model regresi adalah linier, dan berlaku sebaliknya. Berdasarkan tabel ketiga, diperoleh nilai Sig. = 0,140 yang berarti > kriteria signifikan (0,05), dengan demikian model persamaan regresi berdasarkan data penelitian adalah tidak signifikan artinya, model regresi linier tidak memenuhi kriteria linieritas.
  • Tabel keempat menginformasikan model persamaan regresi yang diperoleh dengan koefisien konstanta dan koefisien variabel yang ada di kolom Unstandardized Coefficients B. Berdasarkan tabel ini diperoleh model persamaan regresi :
    Y =38,256 + 0,229 X1

Contoh soal regresi dan perhitungan korelasi regresi, regresi berganda, regresi linear, regresi spss, regresi logistik, logistik regresi, regresi linier berganda, analisis regresi berganda, regresi linier sederhana, model regresi, persamaan regresi, regresi statistik, statistik regresi, jurnal regresi, analisis regresi linear, analisis regresi sederhana, analisis regresi spss, penelitian regresi, contoh analisis regresi, contoh regresi berganda

Beberapa referensi lainnya mengenai olah data statistik khususnya mengenai regresi yang dapat anda pelajari juga dibaca pada link berikut;
- http://www.jonathansarwono.info/regresi/regresi.htm
- http://www.regresi.com/uploads/5/9/4/2/5942698/contoh_hasil.pdf

Read More

Excel - A Regression Example

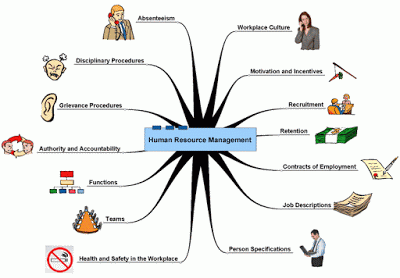
Excel - A Regression Example

Simple linear regression analysis can be easily completed using Excel. The Data Analysis... option of the Tools menu provides what's necessary. If that option is not available in the Excel you are running, you can add it by selecting the Add-Ins... options of the Tools menu.

The example we'll use is from pages 27-30 of Avery and Burkhart, 5th Edition. It will be helpful to follow along in the text as you proceed though this Excel example. An Excel file with the data for the example is available. There are 62 observations of basal area growth and crown volume. We wish to see if basal area growth can be predicted from crown volume based on a simple linear relationship. A portion of the data as it appears in an Excel worksheet appears below.

To plot "BA_GRO" versus "CRWN_VOL" select the data (including labels - cells A1:B63) and choose Chart... under the Insert menu to start up the Chart Wizard. Choose the XY (Scatter) type. Select various options in the Chart Wizard steps to format the graph so it looks like:

From an analysis standpoint you should use this plot to examine whether the assumptions of the technique you intend to use are satisifed for these data. For simple linear regression those assumptions include linearity and constant variance.

Given you are satisfied regarding an initial appraisal of assumptions, you can fit a linear regression to the data by choosing Data Analysis... under the Tools menu and subsequently selecting the Regression Analysis Tool. You will be presented with the following dialog:

Specify the BA_GRO data and label for "Input Y Range:" (B1:B63) and the CRWN_VOL data and label for "Input X Range:" (A1:A63). Check the "Labels" box (since you included data labels in your input ranges), provide a new worksheet name under "Output options" (I used the name Results), and check the Standardized Residuals box. You should obtain the following results (subset shown):

R Square is called coefficient of determination in your text. Intercept is the b₀ term and CRWN_VOL is the slope or b₁ term. The Analysis of Variance table reports the Regression (Reduction in your text) sum-of-squares and the Residual sum-of-squares, the numerator of the residual mean square whose square root is the Standard error of estimate (Standard Error in the Regression Statistics table).

To conduct a residual analysis we want to plot predicted values versus standardized residuals from the output. Select the Predicted BA_GRO label and data and then, holding down on the Ctrl key (Apple key on a Macintosh), select the Standard Residuals label and data:

As before, choose Chart... under the Insert menu to start up the Chart Wizard. Choose the XY (Scatter) type. Once you select various formatting options and insert the chart into your worksheet you will need to complete one extra step. By default the x-axis labels appear in the middle of a residual graph (below a Y value of 0). To move the labels to the bottom of the chart: 1. double click the Y-axis of your chart and 2. under the Scale tab of the resulting dialog specify the axis crosses at the smallest value of Y (-2.5 in the example). Your chart should look like:

The standardized residuals appear to be fairly evenly scattered throughout a horizontal band around 0.0. Hence we might be satisifed regards the assumptions of simple linear regression.

It is possible that an intercept-less equation might be sensible for the "BA_GRO" on "CRWN_VOL" regression. To see this, a new regression would need to be run (checking the "Constant is Zero" box in the Regression dialog box - Excel, in an unfortunate choice of words, chooses to call the intercept parameter "Constant") and the resulting residuals reanalyzed. If an intercept is critical there will be a linear (non-horizontal) trend to the residuals. The two regressions, if both are sound from a residual analysis perspective, can be compared using the Standard Error statistic.

Read More